面白い話、生活に役立つ話、音楽の話など。
メタル、ドラム、などなど。
突然であるが、ハードロック・ヘヴィメタル(HR/HM)というジャンルは、その名称から無用な偏見の対象となることがよくある。これはハードロック・ヘヴィメタルに含まれるごく断片的な部分が、さも全体を指してるかのように錯覚していることに起因する。そういった偏見で一方的にシャッターを閉ざし、一生を終える人は大分損をしているのではないだろうか。
日本では未だ市民権を得ていないのが現状だが、世界的音楽セールスの多くの部分を占めているのはこのハードロック・ヘヴィメタルである。まさにグローバル・スタンダード!
汝、無用な偏見を持つことなかれ!
| ワシ(の写真) |
|---|
 |
| 住まい |
| 中部地方 |
| 興味のある分野 |
|
| 特技 |
|
| 好きなドラマー・参考になるドラマー |
|
| 好きなプロデューサー・ミュージシャン |
|
| 敬意を払う人・賢人・聖人 |
| 音楽の好み |
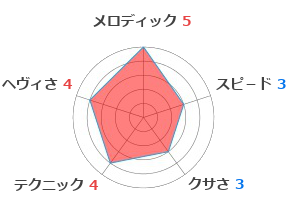 私の好きな音楽でも紹介していますが、ハードロック・ヘヴィメタルを好んで聴いています。1980年代のキンキンなメタルよりも、1990~2000年代のメロディックなメタルの方が好きです。基本的に聴きやすい曲を選ぶことが多く、度を越したものはあまり好きではありません。 私のサイトで紹介している曲も、聴きやすいものが多いので、是非きっかけにどうぞ。 |
プライバシーポリシー・免責事項・連絡先など、各種ポリシーについては以下を参照ください。